[트리] 최소공통조상 LCA 빠르게구하기
① 서로의 깊이를 맞추거나, ②같아지는 노드를 찾을 때, 기존 한단계씩 올려주는 방식에서 2ᵏ씩 올라가 비교하는 방식
→ 기존 자신의 부모노드만 저장해 놓던 방식에서 2ᵏ 번째 위치의 부모노드까지 저장해 둬야한다.
(미리 배열로 저장해야 탐색이 가능하다.)

Step 01) 부모노드 저장 배열 만들기
점화식 활용
- 부모노드 배열 정의
P[K][N] = N번 노드의 2ᵏ 번째 부모의 노드번호
→ P[2][13] = 노드 13의 2² 번째 부모노드 - 점화식 (동적계획법)
P[K][N] = P[K-1][ P[K-1][N] ]
→ P[2][13] = P[1][ P[1][13] ]
점화식에서 N의 2ᵏ 번째 부모노드는 N의 2ᵏ⁻¹번째 부모노드의 2ᵏ⁻¹번째 라는 의미
즉, k=4라고 가정한다면 K의 16번째 부모노드는 K의 8번째 부모노드의 8번째 부모노드라는 의미이다.
K → 2³ ROOT = K→ 2² + 2² => K → 4번째 + 4번째 ROOT
배열에서 k는 `트리의 깊이 > 2ᵏ`을 만족하는 최대값이다.
(만약 전체 노드가 102인데 특정 노드의 2¹⁰²의 노드가 존재할 수 없으므로)
위 트리에서 최대 깊이는 0을 포함한 5이므로 k는 2가 되며 이는 높이를 기준으로 k를 구할 수 있음을 의미한다.
(k가 2일경우 2² = 4 < 5 / k가 3일경우 8 > 5 높이를 초과할수 없으므로 2가 된다.)
초기 세팅 적용
k는 0부터 시작하여 BFS혹은 DFS 알고리즘을 통해 그래프를 탐색하며 초기세팅값을 설정한다.
| k \ index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 (D/BFS) | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 1 (점화식) | null | null | null | null | null | null | null | null | null | null | null | null | null | null | null |
| 2 (점화식) | null | null | null | null | null | null | null | null | null | null | null | null | null | null | null |
ex) 노드 14의 부모노드 배열 정의
높이가 5인 트리에서 k은 2 이므로 아래와 같이 점화식에 2를 대입하여 푼다.
P[2][14]
→ P[1][ P[1][14] ]
↳P[1][14]
→ P[0][ P[0][14] ]
↳P[0][14] = 13
P[0][13] = 11
P[1][11]
→ P[0][ P[0][11] ]
↳P[0][11] = 6
P[0][6] = 3
∴ P[2][14] = 3
이를 그래프에 반영하면 아래와 같다.
| k \ index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 (D/BFS) | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 1 (점화식) | null | null | null | null | null | null | null | null | null | null | 3 | null | null | 11 | null |
| 2 (점화식) | null | null | null | null | null | null | null | null | null | null | null | null | null | 3 | null |
k=2에대한 값만 구해진 것이 아닌 점화식을 통해 거쳐가는 n=1에 대한 노드 11, 13, 14의 값도 각각 초기화된다.
P[2][14]를 구한것처럼 모든 index노드를 점화식으로 반영하여 부모노드 배열을 채운다
| k \ index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 (D/BFS) | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 1 (점화식) | null | null | null | 1 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 6 | 6 | 11 | 11 |
| 2 (점화식) | null | null | null | null | null | null | null | null | null | null | null | 1 | 1 | 3 | 3 |
Step 02) 선택된 두 노드의 깊이 맞추기
초기화된 배열 P를 이용해 기존 한 단계씩 맞춰진 깊이를 2ᵏ 단위로 넘어가면서 맞춘다.
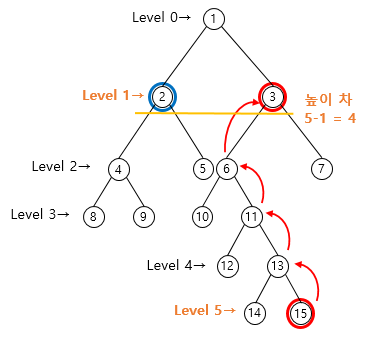
예를들어 노드 2와 노드 15의 깊이를 맞춰본다.
노드 2의 깊이는 1이고 노드 15의 깊이는 5으로 두 노드의 깊이 차는 4이다.
깊이를 맞추기 위해 더 깊이 있는 노드 15의 4번째 부모노드를 P배열을 이용해 찾는다.
4 = 2²이므로 k = 2이고, P[2][15] = 3 이므로 노드 3으로 이동하면 노드 2와 높이를 맞추게 된다.
(1회에 4칸 올라간다.)
만약 높이 차이가 20이라고 가정하면
2² ≤ 20 을 만족하고 k가 최대가되는 만큼 이동하면서 높이차이가 0이될때 까지 반복한다.
즉, 높이 차이가 20일 경우 20은 32보다 작고 16보다 크므로 16으로 계산
이는 2⁴(16) → 2²(4)와 같이 두번 이동하면 된다.
① P[4][N] = 1회에 16칸 점프
→ 높이차 : 20-16 = 4 ∴k=2
② P[2][N] = 1회에 4칸 점프
∴ 2번 만에 높이 20의 차이를 구하게 된다.
ex) 높이 2048 = 2¹¹ → P[11][N]
높이 2048은 2¹¹ 으로 나머지없이 계산되므로 1회만에 탐색한다.
Step 03) 최소 공통 조상 찾기
역시 한단계가 아닌 2ᵏ 단위로 점프하며 서로의 부모노드를 맞춰본다.
k값을 1씩 감소하면서 P배열을 이용해 최초로 두 노드의 부모가 달라지는 값을 탐색한다.
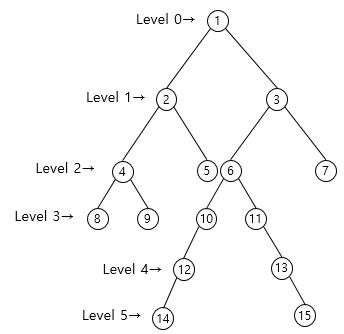
위 트리 그래프에서 두 노드의 높이가 같은 노드 14, 노드 15에 대한 LCA(14, 15)의 최소공통조상을 탐색해보자.
- P[2][14] = 3 == P[2][15] = 3
14의 최대 높이는 2까지이므로 거꾸로 2부터 시작한다.
노드 14와 노드 15에서 k가 2일때 2ᵏ인 4칸씩 올라간다.
두 값이 같으면 최소공통조상을 지난것이므로 k-1 하여 다시 탐색한다.

- P[1][14] = 10 ≠ P[1][15] = 11
두 값이 다르므로 그래프상에서 점프한다( 2ᵏ )
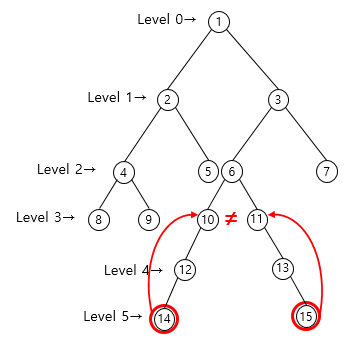
최초로 달라지는 k에 대한 두 노드의 부모노드를 찾아 이동한다.
최초로 달리지는 두 노드의 부모 노드에서 k값을 1회 더 -1 감소시킨 후 다시한번 점화식을 계산한다.
- 노드 10, 노드 11로 이동 후 P[0][10] = 6 == P[0][11] = 6
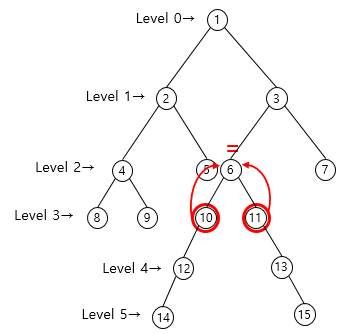
반복문 종료 후, 이동한 두개의 노드가 같은 노드라면 해당 노드가 LCA
두 개의 노드가 다른 노드라면 바로 위 노드가 LCA가 된다. → LCA(16, 17)
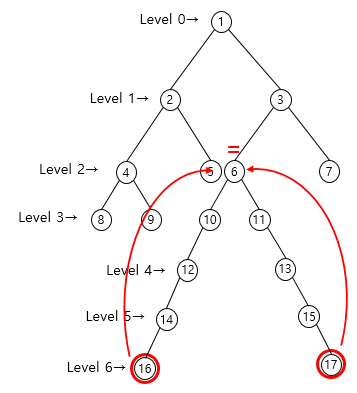
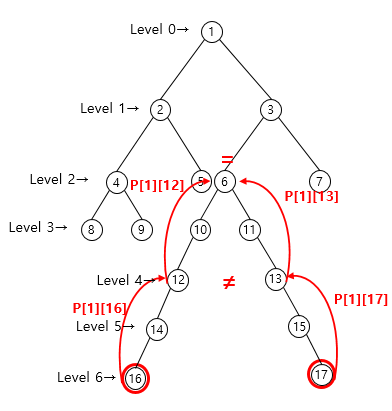
노드 10, 11이 다른노드이기 때문에 바로 위 노드를 뜻하는 P[0][10] 또는 P[0][11] 즉, 노드 6이 최소 공통조상이 된다.


