[정렬 알고리즘] - 병합 정렬과 분할 정복 (logN 개념)

병합정렬

분할정복(divde and conqure) 방식을 사용하여 데이터를 분할한다.
분할된 데이터 집합을 정렬하며 합치는 알고리즘이다.

O(NlogN)의 시간복잡도를 가진다.

 

핵심이론

분할정복방식을 통해 부분 그룹으로 데이터를 나눈다.

 

왜 NlogN인가?

 

정렬하려는 데이터 8개를 3번만에 병렬하여 정렬한다

분할시 logN이 되기 때문에 3회 분할은 log8(2³)로 정의할 수 있다.

 

8개의 데이터를 3회 분할후 정렬했으므로 8개 * log8 회

매 LOOP에서 데이터 그룹에 '8번 Access'하며, 비교하는 작업을 '3회 분할'후 정렬했으므로 8번 * log8 회

• 아래 병합+정렬을 보면 좌측 pointer를 4번 우측 pointer를 4번 이동시키며 비교한다.

이는 8log8 즉 NlogN이 된다.

 

분할 시 logN이 되는 이유

배열의 크기를 반으로 나누는 횟수가 logN에 비례한다. 첫번째 분할 - 배열의 크기를 반으로 나눈다. 한번 분할로 배열이 2개로 나눠진다. 2개로 나뉜 배열 각각에 대해 다시 한번 분할 배열이 4개로 나눠진다. 세번째 분할 - 위 과정을 똑같이 반복하면 8개의 배열로 분할된다. 배열의 크기를 k이라고 가정할 때 각 분할단계의 배열 크기는 k/2 k/4 k/8 즉 k/2ⁿ이 된다. (n은 분할 수행 횟수가 된다.) ex) 배열의 크기가 8일 경우 배열을 1개 단위 까지 나눈다면 8/2ⁿ=1 → 2ⁿ =8 분할 횟수 n = 3이 된다.

 

로그의 정의

로그의 정의는 다음과 같다 만약 k/2ⁿ = 1를 로그 형태로 나타내면 2ⁿ = k → n = log₂(k) 로 나타낼 수 있다. 이렇게 보면 log는 지수(ⁿ)의 값을 얻기 위한 공식으로 사용되었다. log를 함수라고 생각해보면 어떨까? 2ⁿ = k  log(밑,위) = 지수 → log(2, k) = ( ⁿ )  따라서 log는 지수의 값을 얻기 위한 공식 정도로 이해하자!

 

 

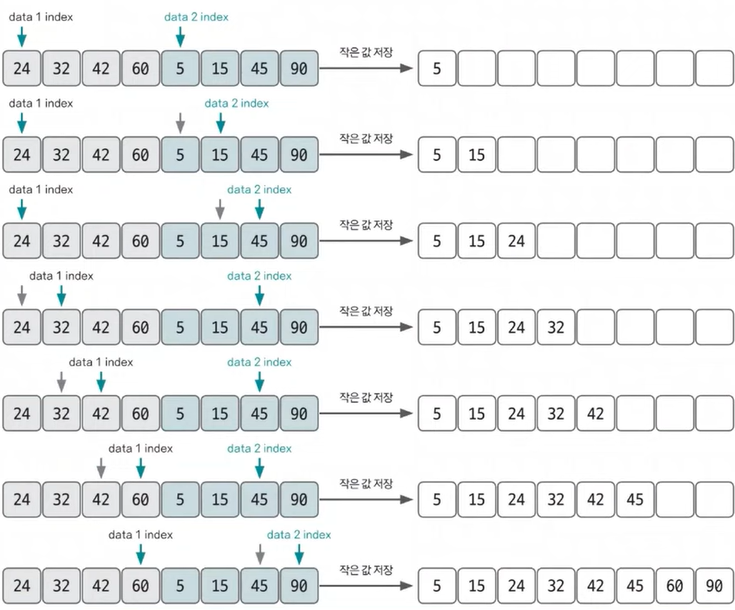
병합과 동시에 정렬하는 법

*2개의 그룹에 대한 병합 원리 필수 숙지

투 포인터 개념을 사용하여 좌/우 그룹을 병합

• 좌측 그룹 포인터 ↔ 우측 그룹 포인터 값을 서로 비교하여 작은(|큰) 값을 결과 배열에 추가한다.
• 포인터를 우측으로 1칸 이동한다. (index++)
  • 우측 그룹 값 결과배열에 추가 : 우측 Pointer를 우측으로 1칸 이동
  • 좌측 그룹 값 결과배열에 추가 : 좌측 Pointer를 우측으로 1칸 이동
  • 위 작업을 반복하여 비교한다
• 좌측 그룹의 모든 포인터값 추출시 정렬 종료 후 남은 데이터는 우측그룹 끝에 순차적으로 저장
  (1개가 남을 수도 있고, 양쪽 모두 정렬된 상태라면 전체가 남을 수도 있다.)

 

응용 예

결과 배열에 저장되는 Pointer 값 대상

• Bubble정렬시 Swap 횟수
• 자동차 경주시 역전횟수