유혁스쿨

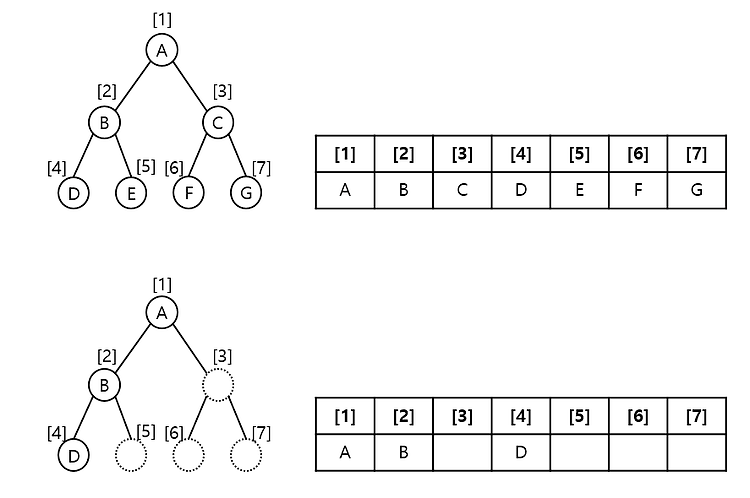
이진 트리 각 노드의 자식의 갯수(차수)가 2 이하로 구성된 트리 트리는 기본적으로 그래프의 표현과 일차원 배열 표현으로 나뉜다. 그래프의 표현으로는 인접리스트를 활용한 BFS, DFS탐색 알고리즘 유형이 있으며 1차원 배열 표현으로는 인덱스 트리와 LCA 유형이 있다. 이진트리는 1차원 배열로 표현하는 인덱스 트리, LCA라고 볼 수 있다. 종류 편향 이진 트리 포화 이진 트리 완전 이진 트리 노드들이 한쪽으로 편향 돼 생성됨 트리의 높이 모두 일정, 리프노드가 꽉참 마지막 레벨 제외하고 노드들이 완전하게 채워짐, 마지막 레벨은 왼쪽부터 채워짐 ⓐ ／ ⓑ ／ ⓒ ／ ⓓ ／ ⓔ ⓐ ∧ ⓑ ⓒ ∧ ∧ ⓓ ⓔⓕ ⓖ ⓐ ∧ ⓑ ⓒ ∧ ⓓ ⓔ 편향 이진 트리에 저장시 탐색속도 저하 및 많은 공간이 낭비된다. 따..

트리 (Tree) 노드와 엣지로 연결된 그래프의 특수한 형태 → 그래프의 표현으로도 Tree를 표현할 수 있다. 순환 구조(Cycle)을 지니지 않고, 1개의 루트 노드가 존재한다. 루트노드를 제외한 노드는 단 1개의 부모노드를 가진다. 트리의 부분트리(SubTree) 역시 트리의 모든 특징을 따른다. 연결된 트리에서 임의의 두 노드를 이어주는 경로는 유일하다. Tree 구성요소 전체 트리 서브트리 ⓐ ← 루트 노드 (부모) ∧ ← 엣지 ⓑ ⓒ ←자식 노드 ∧ ⓓ ⓔ ⓑ ←부모 노드 ∧ ⓓ ⓔ ←리프노드 구성요소 설명 노드 데이터의 index와 value를 표현하는 요소 ] 그래프와 유사 엣지 노드와 노드의 연결 관계를 나타내는 선 루트노드 트리에서 가장 상위에 존재하는 노드 ⓐ 부모노드 두 노드 사이의..

최소신장트리(MST) 그래프에서 모든 노드를 연결할 때 사용된 엣지들의 가중치의 합을 최소로 하는 트리 알고리즘 종류 크루스칼 프림 주요 특징 사이클이 포함되면 가주치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않는다. N개의 노드가 있으면 최소 신장 트리를 구성하는 엣지의 갯수는 항상 N-1개 이다. [그래프] ８ ５ ① ─ ② ─ ⑤ │3 │ 4／2 ③ ─ ④ 13 [엣지리스트] 엣지 ① ② ③ ④ ⑤ ⑥ 노드1 null null null null null null 노드2 null null null null null null 가중치 null null null null null null [유니온파인드리스트] ① ② ③ ④ ⑤ ⑥ null null null null null null Step 01)..

플로이드-워셜 그래프에서 최단거리 구하는 알고리즘 3개(다익스트라, 벨만포드, 플로이드-워셜) 중 1개 기능 특징 시간복잡도(노드수 : V) 모든 노드 간(V³인 이유) 최단경로 탐색 음수 가중치 엣지가 있어도 수행 가능 (단, 음수사이클 x) 동적 계획법 원리를 이용해 알고리즘에 접근 O(V³) (V = 100 / 200 , 1000) (3중 for문으로 코드구성이 간단하기 때문에 쉽게 암기할 수 있음.) A노드에서 B노드 까지 최단 경로를 구했다고 가정했을 때 최단경로 위에 K노드가 존재한다면 그것을 이루는 부분경로 역시 최단경로를 의미한다. 플로이드-워셜 점화식 D[S][E] = Math.min(D[S][E], D[S][K] + D[K][E]) K는 S부터 E까지 도달하는데 위치한 노드이다. S부터..

벨만포드 그래프에서 최단거리를 구하는 알고리즘 기능 특징 시간복잡도 (노드수:V, 엣지수:E) 특정 노드에서 다른 노드까지의 최단경로를 탐색한다. 음수 가중치 엣지가 있어도 수행 가능 전체 그래프에서 음수 사이클 존재 여부 판단 가능 O(VE) 3단계 `그래프`, `엣지리스트`, `최단거리 리스트` 를 활용하여 최단거리를 구한다. [그래프] ８ ５ ① → ② → ⑤ ↓3 ↑-4↙-2 ③ → ④ ７ [엣지리스트] edge 1 2 3 4 5 6 출발노드 null null null null null null 종료노드 null null null null null null 가중치 null null null null null null [정답(최단거리) 리스트] 1 2 3 4 5 null null null null ..

다익스트라 그래프에서 최단 거리를 구하는 알고리즘 기능 특징 (제약조건) 시간 복잡도 (노드 수: V, 엣지 수:E) 출발 노드와 모든 노드간의 최단 거리 탐색 엣지는 모두 양수 O(ElogV) 핵심이론 5단계로 구현한다 [그래프] ８ 15 ① → ② → ⑤ ↓3 ↓4 ↗2 ③ → ④ 13 Step 01) 인접 리스트로 그래프 구현 ① → [ ②, 8 ] [ ③, 3 ] ② → [ ④, 4 ] [ ⑤, 15 ] ③ → [ ④, 13 ] ④ → [ ⑤, 2 ] ⑤ 그래프 데이터를 자료구조 ArrayList 에 저장한다 다익스트라 알고리즘은 인접 행렬로 구현해도 좋으나 시간복잡도 측면 N의 크기가 클 것을 대비해 인접리스트를 선택하여 구현하는 것이 좋다. Step 02) 최단거리 배열 초기화 최단거리 배열 ..

위상정렬 사이클이 없는 방향에서 노드 순서를 갖는 정렬 기능 특징 시간복잡도 (노드수: V, 엣지수: E) 노드간 순서 결정 사이클이 없어야 함 O(V+E) 항상 유일한 값으로 정렬되지 않음 사이클 존재시 노드간 순서를 명확하게 정의 불가 (위상정렬 적용 불가) 핵심 이론 인접리스트 , 진입차수배열 , 위상정렬배열 세가지를 구현한다. 1. 그래프를 인접리스트로 구현 2. 구현된 인접리스트의 진입차수를 계산하여 진입차수 배열에 저장 3. 진입차수배열에서 진입차수가 0인 노드 선택 4. 선택된 노드 위상정렬 배열에 저장 5. 저장된 노드가 가리키는 노드들의 진입차수를 -1 연산 후 저장(선택) 된 노드의 다음노드를 진입차수 배열에서 다시 선택 6. 3 ~ 5 과정을 반복하며 모든 노드가 정렬될 경우 종료 [..

유니온 파인드 여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find연산으로 구성되어 있는 알고리즘 (엄밀히 말하면 그래프 영역이라고 보기에 약간 무리가 있으나 실제로 그래프 문제에서 부분 알고리즘으로 많이 사용됨) find연산이란? 자신의 대표 노드를 찾아주는 연산 핵심이론 union, find 연산을 완벽히 이해하는 것 UNION : 각 노드가 속한 집합을 1개로 합치는 연산 → 노드 a, b가 a ∈ A, b ∈ B일 때 UNION(a,b) 는 A ∪ B를 말함 FIND : 특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산 → 노드 a가 a ∈ A일 때 find(a)는 A집합의 대표노드를 반환 (대..

그래프의 표현 그래프를 표현할때는 대표적으로 엣지리스트, 인접행렬, 인접리스트 3가지 방법으로 표현한다. 그래프 예 ① → ② → ⑤ ↓ ↓ ↗ ③ → ④ 엣지리스트 엣지를 중심으로 그래프를 표현한다. 배열에 출발,도착 노드를 각각 저장하여 엣지를 표현한다. 가중치가 있는 노드의 경우 배열에 가중치를 추가 행으로 함께 저장한다. 가중치 없는 그래프 표현 출발, 도착 2개의 노드만 2개의 배열행을 구성하여 표현한다. ex) 첫번째 행을 [1, 2]로 표현하며 1에서 2로 뻗어가는 엣지를 뜻한다. ⓢ ⓔ 1 2 1 3 3 4 2 4 2 5 4 5 이처럼 방향이 있는 그래프는 순서에 맞게 노드를 배열에 저장하는 방식으로 표현한다. 노드를 배열에 저장하여 엣지를 표현하므로 엣지리스트 라고 한다. 방향이 없는 그..

그래프 노드와 엣지로 구성된 집합. 예) 트리 노드 데이터 표현 단위 엣지 노드를 연결할 때 사용 그래프 알고리즘 종류 유니온 파인드 위상 정렬 다익스트라 벨만-포드 플로이드-워셜 최소 신장 트리 유니온 파인드 그래프의 `사이클 생성 유무`를 판단하는 알고리즘 그래프에서만 쓰이는 알고리즘은 아님 사용 예) `집합에서 대표 노드 탐색` 혹은 `각 원소들을 유니온 하여 하나의 집합으로 통합` ex) 3개의 노드와 2개의 엣지로 구성되었다고 가정했을 때 엣지를 추가할 경우 현재 그래프에 사이클이 생성되는가 → 유니온 파인드로 사이클 생성 여부를 도출한다. 위상 정렬 그래프의 각 노드들을 선형으로 정렬하는 알고리즘 알고리즘 사용 선 조건 사이클이 없어야 한다. 방향(간선)이 있는 그래프이다. ⓐ → ⓑ → ⓒ ..

유클리드 호제법 두 수의 최대 공약수를 구하는 알고리즘 일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수들의 곱으로 표현 할 수 있지만 유클리드 호제법은 조금 더 간단한 방법을 제시한다. 먼저 MOD 연산을 이해 → MOD 연산은 유클리드 호제법에서 최대 공약수를 구하는 핵심 이론 연산 기능 예제 MOD 두 값을 나눈 나머지를 구하는 연산 10 MOD 4 = 2 # 10 % 4 = 2 아래 3단계로 진행한다. 큰 수를 작은 수로 나누는 MOD 연산 수행 앞 단계에서의 작은 수와 MOD 연산 결괏값 (나머지)으로 MOD 연산을 수행 단계 2.를 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택 GCD : Greatest Common Divisor로 최대 공약수의 줄..

서로소란? 공약수가 1외에 없는 수를 뜻함 공약수란? 둘 이상의 정수에서 공통된 약수를 뜻함 공약수와 연관지어 설명하자면 서로소란 둘 이상의 정수에서 공통된 약수중 공약수가 1 외에 없는 수를 말한다. ex) 28과 45은 서로소이다. => 공약수가 1밖에 없기 때문 (두 수는 공통분모, 연관성이 1외에는 없다) 오일러 피(phi) 오일러 피 함수 P[N]의 정의는 1부터 N 까지 범위에서 N과 서로소인 자연수의 갯수를 뜻한다. ex) P[6] = 1~6 범위에서 6과 서로소인 자연수의 갯수 {1, 2, 3, 4, 5, 6} => {1, 5} 2개 에라토스테네스 - 체 이론과 비슷하다. 구하고자 하는 오일러 피의 범위 만큼 배열을 자기 자신 인덱스값으로 초기화 2부터 시작해 현재 배열의 값과 인덱스가 같..

소수란? 자신보다 작은 2개의 자연수를 곱해서 만들수 없는 1보다 큰 자연수 즉, 1과 자기 자신 외에 약수가 존재하지 않는 수를 뜻함 에라토스테네스 체 기법 소수를 구하는 대표적인 판별법 원리 구하고자 하는 소수의 범위만큼 1차원 배열 생성 2번째 부터 시작하며, 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지움 (처음 선택한 숫자는 지우지 않음) 배열 끝까지 2. 을 반복한 후 배열에 남아 있는 모든 수를 출력한다. ▼ 탐색과정 ▼ (1부터 30까지의 수 중 소수를 구한다.) ① 주어진 범위 까지 배열을 생성 (1은 소수가 아니므로 삭제하고 2부터 시작) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 10 ..

그리디 알고리즘 현재 상태에서 보는 선택지 중 최선의 선택지가 전체 선택지 중 최선의 선택지라고 가정하는 알고리즘이다. 즉, 현재 상태에서 선택할 수 있는 방법 중에 최선의 선택을 계속 하다보면 전체 문제에 대한 최선의 선택지가 나올것이라고 가정한다. 예를들어 아래와 같이 1개의 문제에서 5가지의 시점이 존재한다고 가정해본다. ¹ best ² best ³ best ⁴ best ⁵ best 1 ~ 5 총 5가지 시점에서 각 시점의 최선의 해를 선택하여 전체를 풀어나간다. → 위와 같이 풀어 나가다 보면 전체를 푸는 가장 최선의 해가 나올것이라는것이다. 라고 가정하면서 푸는 알고리즘 그리디 알고리즘의 단점 전체 시점을 총 아울렀을 때 항상 최적의 해를 보장하지는 않는다. 코딩 테스트에서는 항상 최적의 해, ..