최소공통조상이란?
트리 그래프에서 임의의 두 노드를 선택했을 때, 선택한 두 노드가 각각 자신을 포함해 거슬러 올라가면서 부모노드를 탐색할 때 처음 공통으로 만나게되는 부모노드를 말한다.
핵심이론
트리의 높이가 크지 않을 때(시간복잡도 ↓)의 예시

ex) 노드4, 노드5의 LCA
→ 루트노드에서 탐색을 시작해 각 노드의 부모노드와 깊이를 배열에 저장한다.
(여기서 탐색은 DFS 혹은 BFS 알고리즘을 사용)
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 부모노드 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 깊이 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
Step 01) 깊이가 다를경우
만약 선택된 두 노드의 깊이가 다른 경우, 더 깊은 노드의 노드를 부모노드로 1개씩 올려주면서 같은 깊이로 맞춘다.
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 부모노드 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 깊이 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
트리 그래프 상에서 노드 15의 깊이가 노드4의 깊이보다 2만큼 더 깊으므로 노드 15의 노드를 부모노드로 1개 올린다.
노드 15의 부모노드는 11이며 해당 index(노드)로 이동한다.
노드 11의 깊이는 노드 4의 깊이보다 1만큼 더 깊으므로 다시한번 부모노드로 1개 올린다.
노드 11의 부모노드는 6이며 해당 index(노드)로 이동한다.
노드 6의 깊이와 노드4의 깊이는 둘다 3으로 동일하기 때문에 깊이를 맞추는것을 중단한다.
이를 그래프로 표현하면 아래와 같다.
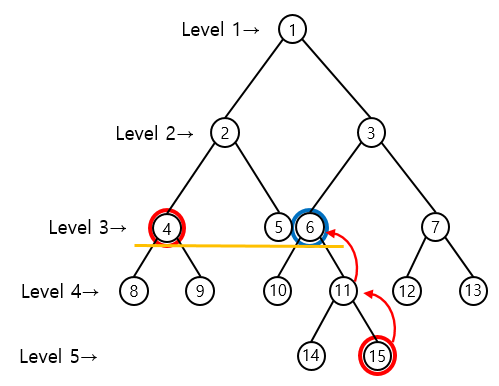
만약 깊이가 높은 노드의 깊이를 기준노드와 맞추다가 해당 노드가 같아지면 최소 공통 조상이므로 탐색을 종료한다.
Step 02) 깊이가 같고 서로다른 노드일 경우
깊이가 같은 상태에서는 두노드가 동시에 부모노드로 올라가면서 두 노드가 같은 노드가 될떄까지 반복한다.
이때 처음 만나는 동일한 부모노드가 최소 공통 조상이 된다.
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 부모노드 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 7 | 11 | 11 |
| 깊이 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 5 |
노드 6의 부모노드는 3 , 노드 4의 부모노드는 2 => 3 != 2 이므로 해당 index위치에서 재탐색
노드 3의 부모노드는 1, 노드 2의 부모느드는 1 => 1 == 1 이므로
결과적으로 노드 4와 노드 15의 최소공통조상은 노드 1이 된다.
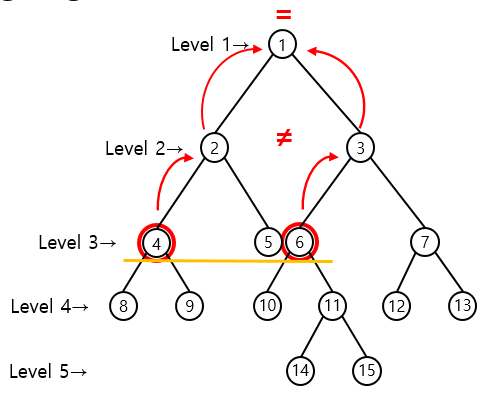
LCA(4, 15) = 1
LCA(3, 15) = 3
위와 같은 방식을 이용하면 최소 공통 조상을 구할 수 있지만, 트리의 높이가 커질 경우, 시간 제약 문제에 직면할 수 있다.
이러한 문제를 해결하기 위해 LCA 알고리즘을 고도화 하여 약간 변형한 형태로 빠르게 구할 수 있다.
다음 포스팅에서 다룰 예정.
'자료구조 알고리즘 코딩테스트 문제풀이 > 알고리즘 - Do it' 카테고리의 다른 글
| 조합과 순열 (0) | 2024.01.20 |
|---|---|
| [트리] 최소공통조상 LCA 빠르게구하기 (0) | 2024.01.18 |
| [트리] 세그먼트(인덱스) 트리 (0) | 2024.01.16 |
| [트리] 이진트리(Binary) (0) | 2024.01.16 |
| [트리] Tree 개념 정리 (1) | 2024.01.15 |