조합 Combination
ₙCᵣ 로 표현하고, 이는 n개의 숫자에서 r개의를 뽑는 경우의 수를 뜻한다.
조합과 비교되는 순열은 ₙPᵣ 로 표현되고 n개의 숫자 중 r개를 뽑아 순서를 고려해 나열할 경우의 수로 말한다.
순열과 조합의 차이는 순서 고려 유무이다.
즉, 조합에서는 데이터 1, 2, 3과 3, 2,1을 동일한 경우로 판단하고 순열은 다른 경우로 판단한다.
일반적으로 코딩테스트의 핵심 알고리즘은 아래와 같다
- 그래프
- DP (동적계획법)
- 인덱스트리
조합은 동적계획법(DP)를 이해하는데 기초가되는 알고리즘으로 코딩테스트에 자주 출제된다.
순열과 조합의 핵심이론
순열
순열의 수학적 공식 ₙPᵣ = n! / (n-r)!
예를들어 데이터 5개 중 2개를 순서대로 선택하는 경우의 수를 구한다고 가정한다.
- 1번째 선택 : 5개의 데이터를 선택할 수 있으므로 5가지 선택 가능
- 2번째 선택 : 1번째에서 선택한 데이터를 제외한 4가지 선택 가능
따라서 5개 중 2개를 고르는 경우의 수는5! / 3! = 5*4*3*2*1 / 3*2*1
총 5*4 = 20개가 된다.
조합
조합의 수학적 공식 ₙCᵣ = n! / (n-r)! * r!
순열과 매우 비슷하며 순열 공식의 분모에 r!을 곱하기만 하면 된다.
여기서 r!이란 순서가 다른 경우의 수를 제거하는 역할을 한다.
예를들어 데이터 5개 중 2개를 순서대로 선택하는 경우의 수를 구한다고 가정한다.
5! / 3! * 2! = (5*4*3*2*1) / (3*2*1) * (2*1)
총 5*4 / 2 = 10개가 된다.
즉, 2개의 데이터. 예를들어 1과 2를 선택할 때와 2와 1을 선택할 때를 1가지 경우의 수로 만들기 위해 2!으로 나누는 것이다. (2개의 데이터는 1과 3 3과 1이 될수도 있고 4와 5 5와 4가 될 수도 있다. )
수학적 관점이 아닌 논리적 관점인 알고리즘적 관점
① 특정 문제 가정
5개의 데이터에서 3개를 선택하는 조합의 경우의 수
| 1 | 2 | 3 | 4 | 5 | ₅C₃ |
② 모든 부분 문제가 해결된 상황이라고 가정한 후 현재 문제 생각하기
먼저 데이터 5개 중 4개를 이미 선택이 완료된 데이터라고 가정한다.
그리고 마지막 데이터의 선택 여부에 따른 경우의 수를 계산한다.
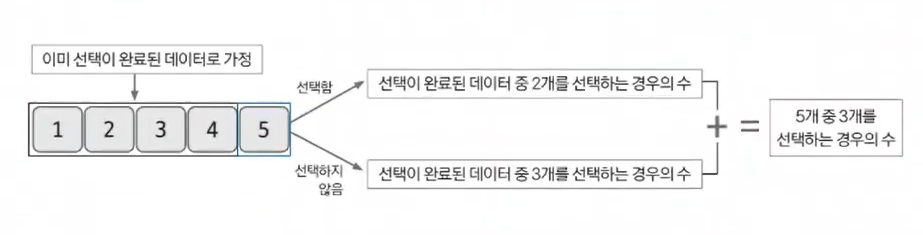
- 마지막 데이터 포함 총 3개의 데이터를 선택 (5 포함)
선택이 완료됐다고 가정한 4개의 데이터 중 2개 선택
(5를 포함하는경우 5를 제외한 2개를 선택하면 3개가 선택되므로) - 마지막 데이터 미포함 총 3개의 데이터를 선택 (5 미포함)
선택이 완료됐다고 가정한 4개의 데이터 중 3개 선택
(5를 미포함 하므로 그대로 3개를 선택)
위 2가지 경우의 수를 합치면 5개 중 3개를 선택하는 경우의 수가 도출된다.
이를 수식으로 표현하면 ₅C₃ = ₄C₃ + ₄C₂ 이고,
수식을 2차원 배열형태로 표현한 점화식으로 표현하면 D[5][3] = D[4][2] + D[4][3] 이 된다.
위 내용을 도출할 때의 고찰
`데이터 4개 중 2개를 선택하는 경우의 수와 데이터 4개 중 3개를 선택하는 경우의 수를 구해야 하는거 아닌가?`
하지만 모든 부분 문제가 해결됐다고 가정해야 한다.
현재 5개중 3개의 경우의 수를 구하는 것이 아니라 궁극적으로 조합과 관련된 점화식을 도출해야 하는 것.
조합도 중요하지만 조합 뿐만 아니라 동적 계획법을 사용해야 하는 부분 문제는 90%가 점화식 도출 싸움 이므로
점화식을 정확하게 도출하면 부분 문제는 프로그램 로직을 이용해 자연스럽게 구할수 있게 된다.
배열 인덱스로 사용된 상수를 변수로 치환하면 아래와 같이 조합에 일반화 된 최종 점화식을 도출할 수 있다.
조합에 일반화 된 점화식 : D[i][j] = D[i-1][j-1] + D[i-1][j]
점화식이란
수열의 일반항을 1개 이상의 앞선 항들을 나타낸 식.
예) 피보나치 수열
'자료구조 알고리즘 코딩테스트 문제풀이 > 알고리즘 - Do it' 카테고리의 다른 글
| D.P. 동적계획법 (0) | 2024.01.22 |
|---|---|
| [트리] 최소공통조상 LCA 빠르게구하기 (0) | 2024.01.18 |
| [트리] 최소공통조상(LCA) 기본 탐색 (0) | 2024.01.17 |
| [트리] 세그먼트(인덱스) 트리 (0) | 2024.01.16 |
| [트리] 이진트리(Binary) (0) | 2024.01.16 |